Suma algebraiczna to istotny termin w matematyce, który odnosi się do wyrażenia składającego się z jednomianów, które mogą być dodawane lub odejmowane. Zrozumienie tego pojęcia jest kluczowe dla dalszego zgłębiania matematyki, szczególnie w kontekście równań i funkcji. Suma algebraiczna pozwala na łączenie różnych składników w jedną całość, co jest niezbędne w wielu dziedzinach matematyki.
W artykule przyjrzymy się bliżej definicji sumy algebraicznej, jej podstawowym składnikom oraz praktycznym przykładom, które pomogą w lepszym zrozumieniu tego zagadnienia. Dowiemy się również, jak suma algebraiczna wpływa na równania i jakie ma zastosowanie w analizie funkcji. Dzięki temu czytelnicy zdobędą solidne podstawy, które ułatwią im dalsze eksplorowanie tematów matematycznych.
Najistotniejsze informacje:- Suma algebraiczna to wyrażenie złożone z jednomianów, które można dodawać lub odejmować.
- Podstawowe składniki sumy algebraicznej to monomy i ich współczynniki.
- Tworzenie sumy algebraicznej polega na łączeniu jednomianów w jedną całość.
- Obliczenia sumy algebraicznej są kluczowe dla rozwiązywania równań i wyrażeń matematycznych.
- Suma algebraiczna ma szerokie zastosowanie w analizie funkcji i innych dziedzinach matematyki.
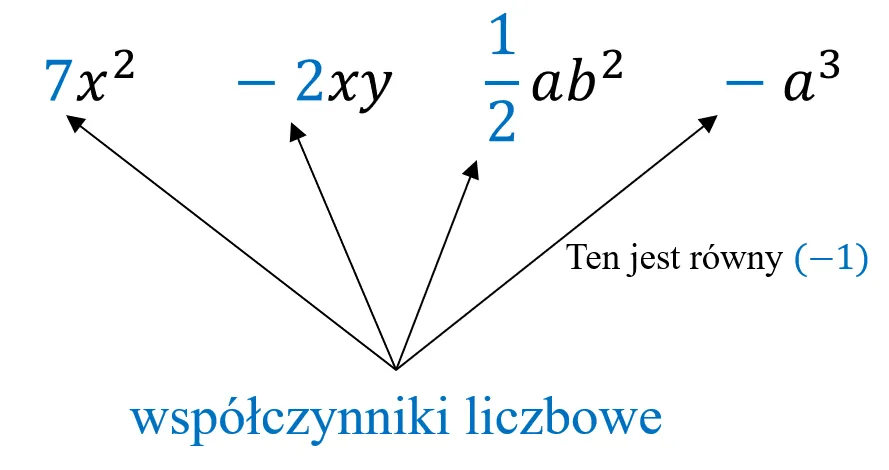
Definicja sumy algebraicznej i jej podstawowe elementy
Suma algebraiczna to wyrażenie matematyczne, które składa się z jednomianów, które mogą być dodawane lub odejmowane. To kluczowy koncept w algebrze, który pozwala na łączenie różnych składników w jedną całość. Zrozumienie tego pojęcia jest istotne dla dalszego zgłębiania bardziej złożonych zagadnień matematycznych, takich jak równania czy funkcje. W kontekście sumy algebraicznej, ważne jest, aby dostrzegać jej znaczenie w rozwiązywaniu problemów matematycznych.
W skrócie, suma algebraiczna to nie tylko zbiór liczb, ale także sposób ich łączenia, co pozwala na tworzenie bardziej złożonych wyrażeń. Dzięki niej można operować na różnych wartościach, co jest niezwykle przydatne w praktycznych zastosowaniach matematyki. W kolejnych sekcjach artykułu przyjrzymy się bliżej składnikom sumy algebraicznej, aby lepiej zrozumieć, jak można ją wykorzystać w różnych kontekstach.
Czym jest suma algebraiczna i jak ją zrozumieć?
Suma algebraiczna to wyrażenie, które można zdefiniować jako wynik dodawania lub odejmowania jednomianów. Każdy jednomian składa się z liczby (współczynnika) i zmiennej (np. x, y), co sprawia, że suma algebraiczna ma różnorodne zastosowania w matematyce. W praktyce oznacza to, że można manipulować tymi wyrażeniami, aby uzyskać pożądane wyniki w obliczeniach.
Aby lepiej zrozumieć sumę algebraiczną, warto zwrócić uwagę na jej matematyczną reprezentację. Zwykle zapisuje się ją w postaci: a + b - c, gdzie a, b i c to jednomiany. Taka forma pozwala na łatwe dodawanie i odejmowanie wartości, co jest podstawą wielu operacji matematycznych. Zrozumienie tego, jak działa suma algebraiczna, jest kluczowe dla dalszego zgłębiania algebry i rozwiązywania bardziej skomplikowanych problemów.
Jakie składniki tworzą sumę algebraiczną?
Suma algebraiczna składa się z kilku podstawowych elementów, które są kluczowe dla jej zrozumienia. Najważniejszymi składnikami są jednomiany, które są pojedynczymi wyrażeniami algebraicznymi, składającymi się z liczby (współczynnika) oraz zmiennej (np. x, y). Współczynniki mogą być liczbami całkowitymi, ułamkowymi lub nawet zmiennoprzecinkowymi, co wpływa na wartość całej sumy. Zrozumienie tych elementów jest niezbędne do prawidłowego formułowania i manipulowania sumami algebraicznymi.
Kolejnym istotnym składnikiem są operacje dodawania i odejmowania, które są podstawowymi działaniami w tworzeniu sumy algebraicznej. Dzięki nim możemy łączyć różne jednomiany w jedną całość, co pozwala na uzyskanie bardziej złożonych wyrażeń. Na przykład, w sumie algebraicznej 3x + 5y - 2, mamy do czynienia z trzema jednomianami, które są łączone za pomocą tych operacji. Zrozumienie, jak te składniki współdziałają, jest kluczowe dla dalszej pracy z sumami algebraicznymi.
Jak tworzyć sumy algebraiczne z jednomianów?
Aby tworzyć suma algebraiczna, należy najpierw zrozumieć, jak łączyć jednomiany. Proces ten polega na dodawaniu lub odejmowaniu tych wyrażeń, co skutkuje nowym wyrażeniem algebraicznym. Kluczowym krokiem jest identyfikacja jednomianów, które chcemy połączyć. Na przykład, jeśli mamy 3x oraz 5y, możemy je dodać, aby uzyskać 3x + 5y. Ważne jest, aby pamiętać, że tylko jednomiany o tych samych zmiennych można łączyć w prosty sposób.
W przypadku, gdy mamy do czynienia z różnymi zmiennymi, suma algebraiczna pozostaje w postaci, w jakiej została zapisana. Na przykład, 3x + 2y nie może być uproszczona dalej, ponieważ x i y są różnymi zmiennymi. Kluczowe jest, aby podczas tworzenia sumy algebraicznej zachować porządek i jasno określić, które jednomiany są dodawane, a które odejmowane. Dzięki temu można łatwo zrozumieć, jak wygląda końcowy wynik.
- 3x - 2y
- 4a + 5b
- 7m - 3n
Przykłady obliczeń sumy algebraicznej w zadaniach
Obliczenia sumy algebraicznej są istotnym elementem pracy z wyrażeniami algebraicznymi. Umożliwiają one łączenie różnych wartości w jedną całość, co jest niezbędne w rozwiązywaniu równań i problemów matematycznych. Na przykład, jeśli mamy wyrażenie 2x + 3x, możemy je połączyć, uzyskując 5x. Takie obliczenia są kluczowe w wielu zadaniach matematycznych, ponieważ pozwalają na uproszczenie wyrażeń i ułatwiają dalsze analizy.Warto również zauważyć, że podczas obliczeń z sumą algebraiczną istotne jest zachowanie poprawności znaków. Na przykład, w wyrażeniu 4y - 2y, musimy pamiętać, aby odjąć odpowiednie wartości, co daje nam wynik 2y. Tego typu umiejętności są niezbędne w algebrze i stanowią fundament dla bardziej zaawansowanych zagadnień matematycznych.
| Wyrażenie algebraiczne | Obliczenia | Wynik |
|---|---|---|
| 3x + 2x | 3x + 2x = 5x | 5x |
| 4a - 2a | 4a - 2a = 2a | 2a |
| 5y + 3y - 2y | (5y + 3y) - 2y = 6y - 2y = 4y | 4y |
| 7m - 3m + 2m | (7m - 3m) + 2m = 4m + 2m = 6m | 6m |
Obliczenia sumy algebraicznej są kluczowe w matematyce, ponieważ pozwalają na łączenie różnych wartości w jedno wyrażenie. Umożliwiają one uproszczenie równań i wyrażeń, co jest niezbędne w wielu zadaniach matematycznych. W przykładzie 3x + 2x, dodajemy dwa jednomiany, co daje nam wynik 5x. Takie operacje są podstawą algebry i pomagają w rozwiązywaniu bardziej złożonych problemów.
Warto również pamiętać, że podczas obliczeń z sumą algebraiczną, istotne jest zachowanie poprawności znaków. Na przykład, w przypadku wyrażenia 4a - 2a, musimy odjąć 2a od 4a, co daje nam wynik 2a. Tego rodzaju umiejętności są niezbędne do dalszej pracy z bardziej skomplikowanymi wyrażeniami algebraicznymi i równaniami.
Jak suma algebraiczna wpływa na równania i wyrażenia?
Suma algebraiczna odgrywa kluczową rolę w rozwiązywaniu równań i uproszczaniu wyrażeń matematycznych. Dzięki możliwości dodawania i odejmowania jednomianów, pozwala na przekształcanie skomplikowanych wyrażeń w prostsze formy. Na przykład, w równaniu 3x + 2x = 5x, suma algebraiczna umożliwia szybkie połączenie podobnych składników, co prowadzi do szybszego rozwiązania problemu. Tego typu operacje są fundamentem algebry i niezbędne w wielu dziedzinach matematyki.
W praktyce, umiejętność manipulowania sumą algebraiczną pozwala na efektywne rozwiązywanie równań wielomianowych oraz ich uproszczenie. Przy pomocy sumy algebraicznej możemy również analizować i przekształcać funkcje, co jest istotne w kontekście bardziej zaawansowanych zagadnień matematycznych. W związku z tym, zrozumienie, jak suma algebraiczna wpływa na równania, jest kluczowe dla każdego ucznia matematyki.
Zastosowanie sumy algebraicznej w analizie funkcji
Suma algebraiczna znajduje zastosowanie w analizie funkcji poprzez umożliwienie łączenia różnych składników, co jest niezbędne w badaniu ich właściwości. Dzięki sumie algebraicznej można formułować funkcje, które są kluczowe w wielu dziedzinach, takich jak ekonomia, fizyka czy inżynieria. Na przykład, funkcja kwadratowa, zapisana jako f(x) = ax² + bx + c, wykorzystuje sumę algebraiczną do przedstawienia relacji między zmiennymi.
W analizie funkcji, suma algebraiczna pozwala na określenie miejsc zerowych, ekstremów oraz zachowania funkcji w różnych przedziałach. Dzięki temu, matematycy i inżynierowie mogą prognozować, jak zmiany w jednym składniku funkcji wpłyną na całość. Zrozumienie tego zastosowania sumy algebraicznej jest kluczowe dla skutecznej analizy i interpretacji danych w różnych kontekstach.
Jak wykorzystać sumę algebraiczną w programowaniu i analizie danych
W dzisiejszym świecie, suma algebraiczna ma zastosowanie nie tylko w matematyce, ale także w programowaniu i analizie danych. W językach programowania, takich jak Python czy R, operacje na sumach algebraicznych są wykorzystywane do przetwarzania danych i tworzenia modeli statystycznych. Na przykład, podczas analizy zbiorów danych, sumy algebraiczne pozwalają na szybkie agregowanie informacji i uzyskiwanie istotnych statystyk, takich jak średnia czy suma całkowita, co jest kluczowe w podejmowaniu decyzji opartych na danych.
Co więcej, w kontekście sztucznej inteligencji i uczenia maszynowego, suma algebraiczna odgrywa fundamentalną rolę w algorytmach optymalizacji. Wiele metod, takich jak regresja liniowa, polega na minimalizacji błędów, które można wyrazić jako sumy algebraiczne. Zrozumienie, jak te sumy wpływają na wyniki modeli, może pomóc programistom w tworzeniu bardziej precyzyjnych i efektywnych algorytmów. W miarę jak technologia się rozwija, umiejętność pracy z sumami algebraicznymi staje się coraz bardziej cenna w różnych dziedzinach, od analizy danych po rozwój oprogramowania.

