Sprawdzanie, czy podana liczba spełnia równanie matematyczne, jest kluczową umiejętnością w matematyce. Proces ten polega na podstawieniu danej liczby w miejsce zmiennej w równaniu oraz obliczeniu wartości wyrażeń po obu stronach. Jeśli wartości te są równe, oznacza to, że liczba spełnia równanie; w przeciwnym razie, nie jest to prawdą. W artykule przedstawimy krok po kroku, jak przeprowadzić tę weryfikację oraz omówimy najczęstsze błędy, które mogą wystąpić podczas tego procesu.
Ważne jest, aby zrozumieć, jak prawidłowo podstawiać liczby i porównywać wyniki, ponieważ pozwala to uniknąć nieporozumień i błędów w obliczeniach. Dzięki naszym wskazówkom i przykładom, nauczysz się, jak skutecznie ocenić, czy dana liczba jest rozwiązaniem równania, co jest niezbędne w dalszym rozwoju umiejętności matematycznych.
Najistotniejsze informacje:
- Podstawienie liczby w miejsce zmiennej jest kluczowym krokiem w weryfikacji równania.
- Porównanie wartości po obu stronach równania pozwala ustalić, czy liczba spełnia równanie.
- Typowe błędy obejmują pomyłki w obliczeniach i niewłaściwe podstawienie wartości.
- Przykłady równań liniowych i kwadratowych ilustrują proces weryfikacji.
- Dokładne sprawdzanie obliczeń może pomóc uniknąć błędów i nieporozumień.
Jak weryfikować, czy liczba x spełnia równanie matematyczne?
Weryfikacja, czy podana liczba spełnia równanie matematyczne, jest podstawową umiejętnością, która ma kluczowe znaczenie w matematyce. Proces ten polega na podstawieniu danej liczby w miejsce zmiennej w równaniu oraz obliczeniu wartości wyrażeń po obu stronach. Jeśli wartości te są równe, oznacza to, że liczba spełnia równanie; w przeciwnym razie, nie jest to prawdą. Umiejętność ta jest niezbędna nie tylko w szkole, ale również w codziennym życiu, gdzie często spotykamy się z różnymi problemami matematycznymi.
Aby skutecznie weryfikować równania, należy znać kilka podstawowych kroków. Proces ten można podsumować w trzech etapach: podstawienie wartości zmiennej, obliczenie wartości wyrażeń po obu stronach oraz porównanie wyników. Zrozumienie tego procesu pozwala na uniknięcie błędów i nieporozumień, co jest niezwykle ważne w dalszym rozwijaniu umiejętności matematycznych.
Krok po kroku: podstawienie liczby do równania dla weryfikacji
Podstawienie liczby do równania jest pierwszym i kluczowym krokiem w procesie weryfikacji. Aby to zrobić, należy zidentyfikować zmienną w równaniu i zastąpić ją wartością, którą chcemy sprawdzić. Na przykład, jeśli mamy równanie 5x + 4 = 2x + 3 i chcemy sprawdzić, czy liczba x = 1 spełnia to równanie, podstawiamy 1 w miejsce x. W ten sposób uzyskujemy 5(1) + 4 po lewej stronie i 2(1) + 3 po prawej stronie.
Po podstawieniu liczby, następnym krokiem jest przeprowadzenie obliczeń. W naszym przykładzie, lewa strona równania daje 5(1) + 4 = 9, a prawa strona to 2(1) + 3 = 5. Wartości te są różne, co oznacza, że liczba x = 1 nie spełnia równania. Warto pamiętać, że poprawne wykonanie obliczeń jest kluczowe dla uzyskania prawidłowego wyniku.
- Identyfikuj zmienną w równaniu, którą chcesz sprawdzić.
- Podstaw wartość liczby w miejsce zmiennej w równaniu.
- Oblicz wartości wyrażeń po obu stronach równania.
- Porównaj wyniki, aby ustalić, czy liczba spełnia równanie.
Porównanie wyników: jak sprawdzić równość obu stron równania
Po podstawieniu wartości do równania kluczowym krokiem jest porównanie wyników uzyskanych po obliczeniach. Aby ustalić, czy liczba spełnia równanie, należy sprawdzić, czy wartości po lewej i prawej stronie równania są równe. Jeśli obie wartości są identyczne, to oznacza, że liczba x spełnia równanie. W przeciwnym razie, liczba nie jest rozwiązaniem równania.
Równania są fundamentem matematyki, a umiejętność ich weryfikacji jest niezbędna w wielu dziedzinach. Porównując wyniki, można nie tylko potwierdzić poprawność obliczeń, ale także zrozumieć, jak różne wartości wpływają na równanie. Równość stron równania jest istotna, ponieważ pozwala na analizowanie i rozwiązywanie problemów matematycznych w sposób systematyczny i logiczny.
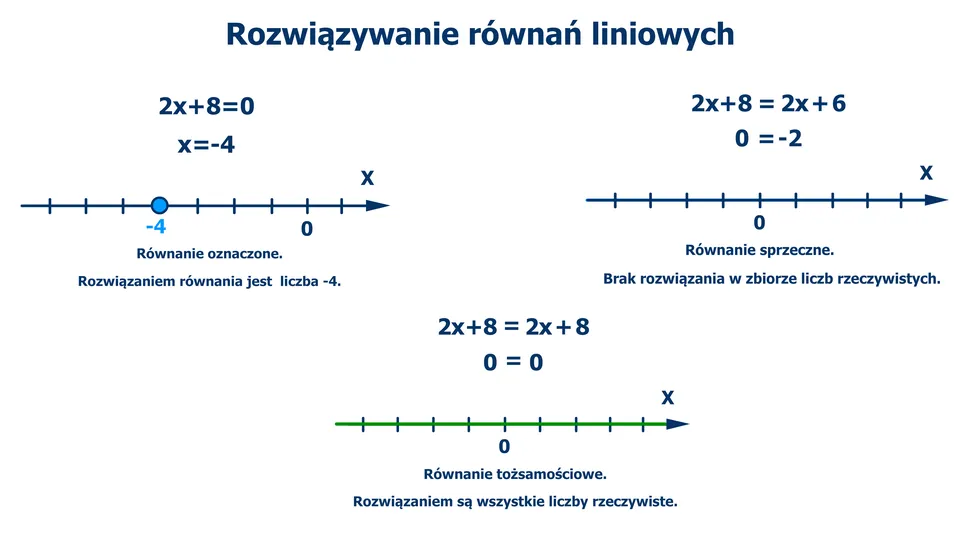
Najczęstsze błędy przy weryfikacji równań matematycznych
Podczas weryfikacji równań matematycznych mogą wystąpić różne typowe błędy, które mogą prowadzić do nieprawidłowych wyników. Często zdarza się, że uczniowie popełniają błędy arytmetyczne, takie jak pomyłki w dodawaniu lub mnożeniu. Ponadto, niewłaściwe podstawienie wartości zmiennej lub błędne zrozumienie równania również mogą prowadzić do błędnych wniosków.
Aby uniknąć tych powszechnych błędów, warto wdrożyć kilka prostych strategii. Po pierwsze, zawsze warto podwójnie sprawdzić swoje obliczenia, aby upewnić się, że nie popełniono błędów arytmetycznych. Po drugie, warto czytać równanie uważnie, aby zrozumieć, co oznaczają poszczególne zmienne. Użycie kalkulatora lub narzędzi do obliczeń online może również pomóc w uniknięciu pomyłek.
Jak unikać typowych pułapek w obliczeniach matematycznych?
Aby uniknąć typowych pułapek w obliczeniach matematycznych, warto stosować kilka sprawdzonych strategii. Po pierwsze, zawsze warto sprawdzać swoje obliczenia po ich wykonaniu. Nawet drobne pomyłki arytmetyczne mogą prowadzić do błędnych wyników, dlatego warto poświęcić chwilę na ich weryfikację. Po drugie, korzystanie z szacowania wyników przed wykonaniem dokładnych obliczeń może pomóc w zidentyfikowaniu ewentualnych błędów na wczesnym etapie.
Trzecią strategią jest użycie różnych metod obliczeniowych. Na przykład, jeśli masz równanie do rozwiązania, spróbuj je rozwiązać na kilka sposobów, aby upewnić się, że uzyskujesz te same wyniki. Ponadto, warto korzystać z narzędzi takich jak kalkulatory, które mogą pomóc w obliczeniach i minimalizować ryzyko błędów. Wreszcie, systematyczne podejście do rozwiązywania problemów matematycznych, polegające na dokładnym śledzeniu każdego kroku, również może znacznie zwiększyć dokładność obliczeń.
Analiza konkretnych przypadków: równania liniowe i kwadratowe
Równania liniowe to jedne z najprostszych do zrozumienia i weryfikacji. Na przykład, rozważmy równanie 2x + 3 = 7. Aby sprawdzić, czy liczba x = 2 spełnia to równanie, podstawiamy 2 w miejsce x. Lewa strona równania daje 2(2) + 3 = 7, co jest równe prawej stronie, więc liczba x = 2 spełnia to równanie.
Równania kwadratowe są nieco bardziej złożone, ale również można je skutecznie weryfikować. Na przykład, dla równania x² - 4 = 0, sprawdźmy, czy x = 2 jest rozwiązaniem. Podstawiając 2, otrzymujemy 2² - 4 = 0, co jest równe 0, więc liczba x = 2 spełnia równanie. Innym przypadkiem może być równanie x² - 5x + 6 = 0, którego rozwiązania to x = 2 i x = 3. Podstawiając te wartości, możemy potwierdzić, że obie spełniają równanie.
| Równanie | Podstawiona wartość | Wynik lewej strony | Wynik prawej strony | Spełnia równanie? |
| 2x + 3 = 7 | 2 | 7 | 7 | Tak |
| x² - 4 = 0 | 2 | 0 | 0 | Tak |
| x² - 5x + 6 = 0 | 3 | 0 | 0 | Tak |
Jak rozwijać umiejętności matematyczne poprzez praktykę i gry
Rozwój umiejętności matematycznych, w tym weryfikacji równań, można wspierać poprzez praktykę i gry edukacyjne. Użycie gier matematycznych, takich jak Sudoku czy różne łamigłówki logiczne, może znacząco poprawić zdolności analityczne oraz umiejętność rozwiązywania problemów. Te aktywności nie tylko uczą, jak sprawdzać, czy podana liczba x spełnia równanie, ale także rozwijają zdolność do myślenia krytycznego i kreatywnego w kontekście matematyki.
Dodatkowo, warto korzystać z aplikacji mobilnych i platform edukacyjnych, które oferują interaktywne ćwiczenia i quizy. Takie narzędzia umożliwiają personalizację nauki oraz dostosowanie poziomu trudności do indywidualnych potrzeb ucznia. Regularne korzystanie z takich zasobów może prowadzić do znacznej poprawy w umiejętności matematycznych, co w dłuższej perspektywie przynosi korzyści nie tylko w szkole, ale również w codziennym życiu oraz w karierze zawodowej.

